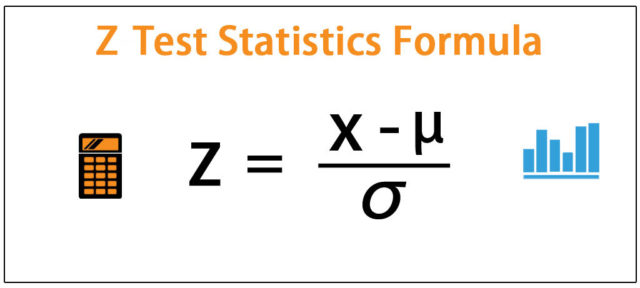Z-Test definition –
A statistical test that is used to determine if two population means are different when the variances are known and the sample size is large is known as Z-test. The statistic is assumed to have a normal distribution and nuisance parameters like a standard deviation in order for an accurate z-test to be performed. A number that represents how many standard deviations are above or below the mean population, a score derived from a z-test is called Z-statistic or Z-score.
Important points to be noted
- A statistical test which is used to determine if two population means are different when the variances are known and the sample size is large is called Z-test
- The use of this test can be done to test hypotheses in which the z-test follows a normal distribution.
- A number that represents the result from the Z-test calculation is known as Z-statistic or Z-score.
- Z-test is a bit similar to T-tests but the T-test is best performed when an experiment has a small sample size.
- In Z-tested standard deviation in known whereas in T-test it is unknown.
How Z-tests work
Z-tests include a one-sample location test, a two-sample location test, a paired difference test and a maximum likelihood estimate in the examples. Z-tests and T-tests are similar but t-tests are best when an experiment has a small sample size. Also, assume the standard deviation I known in Z-test whereas it is unknown un T-tests. When the standard deviation of the population is unknown only then the assumption of the sample variance equalling the population variance can be made.
Hypothesis Test
The Z-statistic follows a normal distribution so a Z-test is also known as a hypothesis test. Z-test is used when there are more than 30 samples because under the central limit theorem as the number of samples is more the samples are considered to be approximately normally distributed. The null and alternative hypotheses, alpha and Z-score should be stated when conducting a Z-test followed by the test statistic calculation and the results with the conclusion stated.
Z-test Example of one sample
An investor wants to calculate whether the average daily return of the stock is more than 1%. A random sample of 50 returns is calculated and it has an average of 2%. Let’s assume the standard deviation of return is 2.5%. so the null hypothesis is when the average or mean is equal to 3%.
Whereas the alternative hypothesis is whether the mean return is greater than 3%. Assume alpha of 0.05% is selected with a two-tailed test, so there is 0.025% of the sample in each tail and the alpha has a value of 1.96 or -1.96. The null hypothesis is rejected if the value of z is less than -1.96.
By subtracting the value of the average of the daily return selected for the test or 1% in the above example from the observed average of samples the value of the Z-test is calculated. Now divide the resulting value by the standard deviation divided by the square root of the number of observed values. So the calculation of the test statistic is 2.83 or (0.02-0.01) / (0.025 / (50)^(1/2)). Since Z is greater than 1.96 the investor rejects the null hypothesis and concludes that the average daily return is greater than 1%.